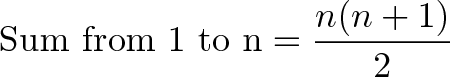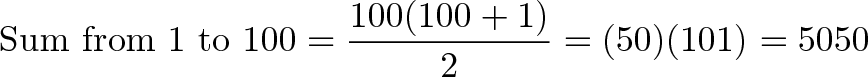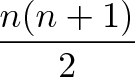Most Influential Psychologists: A Look at Eminent Thinkers in Psychology

These individuals are not only some of the best-known thinkers in psychology, they also played an important role in psychology's history and made important contributions to our understanding of human behavior. This list is not an attempt to identify who was the most influential or which school of thought was best. Instead, this list offers a glimpse of some of the theoretical outlooks that have influenced not only psychology, but also the larger culture in which we live.

B. F. Skinner

In the 2002 study ranking the 99 most eminent psychologists of the 20th century, B.F. Skinner topped the list. Skinner's staunch behaviorism made him a dominating force in psychology and therapy techniques based on his theories are still used extensively today, including behavior modification and token economies.

Sigmund Freud

When people think of psychology, many tend to think of Freud. His work supported the belief that not all mental illnesses have physiological causes and he also offered evidence that cultural differences have an impact on psychology and behavior. His work and writings contributed to our understanding of personality, clinical psychology, human development, and abnormal psychology.

Albert Bandura

Bandura's work is considered part of the cognitive revolution in psychology that began in the late 1960s. His social learning theory stressed the importance of observational learning, imitation, and modeling. "Learning would be exceedingly laborious, not to mention hazardous, if people had to rely solely on the effects of their own actions to inform them what to do," Bandura explained in his 1977 bookSocial Learning Theory.

Jean Piaget

Jean Piaget's work had a profound influence on psychology, especially our understanding children's intellectual development. His research contributed to the growth of developmental psychology, cognitive psychology, genetic epistemology, and education reform. Albert Einstein once described Piaget's observations on children's intellectual growth and thought processes as a discovery "so simple that only a genius could have thought of it." 

Carl Rogers

Carl Rogers placed emphasis on human potential, which had an enormous influence on both psychology and education. He became one of the major humanist thinkers and an eponymous influence in therapy with his "Rogerian therapy." As described by his daughter Natalie Rogers, he was "a model for compassion and democratic ideals in his own life, and in his work as an educator, writer, and therapist." 

William James

Psychologist and philosopher William James is often referred to as the father of American psychology. His 1200-page text, The Principles of Psychology, became a classic on the subject and his teachings and writings helped establish psychology as a science. In addition, James contributed to functionalism, pragmatism, and influenced many students of psychology during his 35-year teaching career. 

Erik Erikson

Erik Erikson's stage theory of psychosocial development helped create interest and research on human development through the lifespan. An ego psychologist who studied with Anna Freud, Erikson expanded psychoanalytic theory by exploring development throughout the life, including events of childhood, adulthood, and old age.

Ivan Pavlov

Ivan Pavlov was a Russian physiologist whose research on conditioned reflexes influenced the rise of behaviorism in psychology. Pavlov's experimental methods helped move psychology away from introspection and subjective assessments to objective measurement of behavior.

Lev Vygotsky

Vygotsky was a contemporary of some better known psychologists including Piaget, Freud, Skinner, and Pavlov, yet his work never achieved the same eminence during his lifetime. This is largely because many of his writing remained inaccessible to the Western world until quite recently. It was during the 1970s that many of his writings were translated from Russian, but his work has become enormously influential in recent decades, particularly in the fields of educational psychology and child development.

While his premature death at age 38 put a halt to his work, he went on to become one of the most frequently cited psychologists of the 20th-century. 

Easiest Way to Evaluate Number from 1-100

There’s a popular story that Gauss, mathematician extraordinaire, had a lazy teacher. The so-called educator wanted to keep the kids busy so he could take a nap; he asked the class to add the numbers 1 to 100.

Gauss approached with his answer: 5050. So soon? The teacher suspected a cheat, but no. Manual addition was for suckers, and Gauss found a formula to sidestep the problem:

Let’s share a few explanations of this result and really understand it intuitively. For these examples we’ll add 1 to 10, and then see how it applies for 1 to 100 (or 1 to any number).

Technique 1: Pair Numbers

Pairing numbers is a common approach to this problem. Instead of writing all the numbers in a single column, let’s wrap the numbers around, like this:

1  2  3  4  5
10 9  8  7  6

An interesting pattern emerges: the sum of each column is 11. As the top row increases, the bottom row decreases, so the sum stays the same.

Because 1 is paired with 10 (our n), we can say that each column has (n+1). And how many pairs do we have? Well, we have 2 equal rows, we must have n/2 pairs.

which is the formula above.

Wait — what about an odd number of items?

Ah, I’m glad you brought it up. What if we are adding up the numbers 1 to 9? We don’t have an even number of items to pair up. Many explanations will just give the explanation above and leave it at that. I won’t.

Let’s add the numbers 1 to 9, but instead of starting from 1, let’s count from 0 instead:

0  1  2  3  4
9  8  7  6  5

By counting from 0, we get an “extra item” (10 in total) so we can have an even number of rows. However, our formula will look a bit different.

Notice that each column has a sum of n (not n+1, like before), since 0 and 9 are grouped. And instead of having exactly n items in 2 rows (for n/2 pairs total), we have n + 1 items in 2 rows (for (n + 1)/2 pairs total). If you plug these numbers in you get:

which is the same formula as before. It always bugged me that the same formula worked for both odd and even numbers – won’t you get a fraction? Yep, you get the same formula, but for different reasons.

Technique 2: Use Two Rows

The above method works, but you handle odd and even numbers differently. Isn’t there a better way? Yes.

Instead of looping the numbers around, let’s write them in two rows:

1  2  3  4  5  6  7  8  9  10
10 9  8  7  6  5  4  3  2  1

Notice that we have 10 pairs, and each pair adds up to 10+1.

The total of all the numbers above is

But we only want the sum of one row, not both. So we divide the formula above by 2 and get:

Now this is cool (as cool as rows of numbers can be). It works for an odd or even number of items the same!

Technique 3: Make a Rectangle

I recently stumbled upon another explanation, a fresh approach to the old pairing explanation. Different explanations work better for different people, and I tend to like this one better.

Instead of writing out numbers, pretend we have beans. We want to add 1 bean to 2 beans to 3 beans… all the way up to 5 beans.

x
x x
x x x
x x x x
x x x x x

Sure, we could go to 10 or 100 beans, but with 5 you get the idea. How do we count the number of beans in our pyramid?

Well, the sum is clearly 1 + 2 + 3 + 4 + 5. But let’s look at it a different way. Let’s say we mirror our pyramid (I’ll use “o” for the mirrored beans), and then topple it over:

x                 o      x o o o o o
x x             o o      x x o o o o
x x x         o o o  =>  x x x o o o
x x x x     o o o o      x x x x o o
x x x x x o o o o o      x x x x x o

Cool, huh? In case you’re wondering whether it “really” lines up, it does. Take a look at the bottom row of the regular pyramid, with 5′x (and 1 o). The next row of the pyramid has 1 less x (4 total) and 1 more o (2 total) to fill the gap. Just like the pairing, one side is increasing, and the other is decreasing.

Now for the explanation: How many beans do we have total? Well, that’s just the area of the rectangle.

We have n rows (we didn’t change the number of rows in the pyramid), and our collection is (n + 1) units wide, since 1 “o” is paired up with all the “x”s.

Notice that this time, we don’t care about n being odd or even – the total area formula works out just fine. If n is odd, we’ll have an even number of items (n+1) in each row.

But of course, we don’t want the total area (the number of x’s and o’s), we just want the number of x’s. Since we doubled the x’s to get the o’s, the x’s by themselves are just half of the total area:

And we’re back to our original formula. Again, the number of x’s in the pyramid = 1 + 2 + 3 + 4 + 5, or the sum from 1 to n.

Technique 4: Average it out

We all know that

average = sum / number of items

which we can rewrite to

sum = average * number of items

So let’s figure out the sum. If we have 100 numbers (1…100), then we clearly have 100 items. That was easy.

To get the average, notice that the numbers are all equally distributed. For every big number, there’s a small number on the other end. Let’s look at a small set:

1 2 3

The average is 2. 2 is already in the middle, and 1 and 3 “cancel out” so their average is 2.

For an even number of items

1 2 3 4

the average is between 2 and 3 – it’s 2.5. Even though we have a fractional average, this is ok — since we have an even number of items, when we multiply the average by the count that ugly fraction will disappear.

Notice in both cases, 1 is on one side of the average and N is equally far away on the other. So, we can say the average of the entire set is actually just the average of 1 and n: (1 + n)/2.

Putting this into our formula

And voila! We have a fourth way of thinking about our formula.

So why is this useful?

Three reasons:

1) Adding up numbers quickly can be useful for estimation. Notice that the formula expands to this:

Let’s say you want to add the numbers from 1 to 1000: suppose you get 1 additional visitor to your site each day – how many total visitors will you have after 1000 days? Sincethousand squared = 1 million, we get million / 2 + 1000/2 = 500,500.

2) This concept of adding numbers 1 to N shows up in other places, like figuring out the probability for the birthday paradox. Having a firm grasp of this formula will help your understanding in many areas.

3) Most importantly, this example shows there are many ways to understand a formula. Maybe you like the pairing method, maybe you prefer the rectangle technique, or maybe there’s another explanation that works for you. Don’t give up when you don’t understand — try to find another explanation that works. Happy math.

By the way, there are more details about the history of this story and the technique Gauss may have used.

Variations

Instead of 1 to n, how about 5 to n?

Start with the regular formula (1 + 2 + 3 + … + n = n * (n + 1) / 2) and subtract off the part you don’t want (1 + 2 + 3 + 4 = 4 * (4 + 1) / 2 = 10).

Sum for 5 + 6 + 7 + 8 + … n = [n * (n + 1) / 2] – 10

And for any starting number a:

Sum from a to n = [n * (n + 1) / 2] – [(a - 1) * a / 2]

We want to get rid of every number from 1 up to a – 1.

How about even numbers, like 2 + 4 + 6 + 8 + … + n?

Just double the regular formula. To add evens from 2 to 50, find 1 + 2 + 3 + 4 … + 25 and double it:

Sum of 2 + 4 + 6 + … + n = 2 * (1 + 2 + 3 + … + n/2) = 2 * n/2 * (n/2 + 1) / 2 = n/2 * (n/2 + 1)

So, to get the evens from 2 to 50 you’d do 25 * (25 + 1) = 650

How about odd numbers, like 1 + 3 + 5 + 7 + … + n?

That’s the same as the even formula, except each number is 1 less than its counterpart (we have 1 instead of 2, 3 instead of 4, and so on). We get the next biggest even number (n + 1) and take off the extra (n + 1)/2 “-1″ items:

Sum of 1 + 3 + 5 + 7 +  … + n = [(n + 1)/2 * ((n + 1)/2 + 1)] – [(n + 1) / 2]

To add 1 + 3 + 5 + … 13, get the next biggest even (n + 1 = 14) and do

[14/2 * (14/2 + 1)] – 7 = 7 * 8 – 7 = 56 – 7 = 49

Combinations: evens and offset

Let’s say you want the evens from 50 + 52 + 54 + 56 + … 100. Find all the evens

2 + 4 + 6 + … + 100 = 50 * 51

and subtract off the ones you don’t want

2 + 4 + 6 + … 48 = 24 * 25

So, the sum from 50 + 52 + … 100 = (50 * 51) – (24 * 25) = 1950

Phew! Hope this helps.

Ruby nerds: you can check this using

(50..100).select {|x| x % 2 == 0 }.inject(:+)
1950

Learning in Music

                                             


Music, rhythm, and rhyme are great for learning and memory. Quick, which months have thirty days? If you're like me, you have to say the rhyme we all learned in school to be sure. Many kindergarteners can't say their ABC's, but they can sing them. People use music and rhythm for memorizing all sorts of lists, from the books of the Bible to the digits of pi.

Why Learn English Through Songs and Music?

So what is it about songs that make them such effective English language learning tools?

• It works. There is considerable scientific evidence that demonstrates how music can help second language learners acquire grammar and vocabulary and improve spelling. Then there is the so-called “Mozart Effect”, the concept that listening to classic musical boosts the performance of mental tasks like learning.
• Everyday language and colloquial speech. Songs and music almost always contain a lot of useful vocabulary, phrases and expressions. And since the intended audience is native speakers, songs and music include up-to-date language and colloquialisms. The language used in songs is casual and actually usable, if you pick the right music.
• Get familiar with the sound of English. Listening to songs will also allow you to focus on your pronunciation and understanding of the English language’s rhythm, tone and beat.
• Get English stuck inside your head. Many of the words and sound patterns within a song are repetitive and this makes it easier for them to stick in your mind. You probably already know this. Music has an uncanny ability of getting stuck in our heads. Tunes and lyrics will often infiltrate our thoughts and play over and over in our minds. All of which will help you to learn English through songs as you easily memorize vocabulary and phrases. In fact, after a short period of time you will find it almost impossible to forget them.
• Songs are emotional. Our relationship with music is deep, powerful and hugely rewarding. It is a key that unlocks our emotions, influences our moods and enhances our mental and physical well-being. When something is emotional, then of course it is also easier to remember.
• Music is an easy habit. One reason people find language learning difficult is they don’t have an extra minute in the day to devote to their studies. But when you’re learning English through songs, you don’t need to set aside too much time because you can take the music with you wherever you go. You can have English songs playing in the car, the kitchen and the shower. And by picking music you like, you can listen to the same material over and over again, without becoming bored.
• Music teaches you English culture. Music gives you insight into English-speaking culture and how English-speaking people think and feel. Familiarity with popular songs and artists gives you something to talk about with your English-speaking friends.

        Music is a very effective tool that should play a larger role in the EFL/ESL classroom  because it offers a great variety that appeals to the students. Most children enjoy music  and therefore it should increase their interest in learning a new language in a very  entertaining way. Educators need to be willing to incorporate music in their lessons in  order to better enhance their students’ learning. 

        Music can be used to remove language barriers and should be implemented as 

early as the first grade. More music in every language classroom will inspire more 

students to become creative and independent. Music will allow educators and their 

students to understand each other and connect in a new way.

Self-confidence VS Self-esteem

The terms self-esteem and self-confidence are often used interchangeably when referring to how one feels about themselves. Although they are very similar, they are two different concepts. It is important to understand their roles when looking to improve your overall sense of self.

What is Self-Esteem?

Self-esteem refers to how you feel about yourself overall; how much esteem, positive regard or self-love you have. Self-esteem develops from experiences and situations that have shaped how you view yourself today.

Self-confidence is how you feel about your abilities and can vary from situation to situation. I may have healthy self-esteem, but low confidence about situations involving math (this is true).

When you love yourself, your self-esteem improves, which makes you more confident. When you are confident in areas of your life, you begin to increase your overall sense of esteem. You can work on both at the same time.

What Does Low Self-Esteem Look Like?

A friend told me she has low self-esteem; she constantly feels “I’m not good enough.” This concept has developed over her entire life. She has been in a series of unhealthy relationships, is frequently belittled by her boss, and constantly tells herself “I suck, I’m not worth it.” Recognizing she has this negative script, she is now better able to change it.

On the positive side, she is confident about being an amazing chef, a caring friend, and having the ability to be super-organized. She knows and believes this about herself and feels confident in these areas. By focusing on the things she is confident in and working on changing her negative self-talk, she is improving both her self-esteem and self-confidence.

Ideas for Improving Self-Esteem and Self-Confidence

If you are having trouble finding areas you are confident in, try these tips.

• Think of qualities others say you excel in. Even if you believe them slightly, this is a step in the right direction.
• Stop the negative chatter. Shut it up! Start to think of contradictions to these statements.
• Would you say it to a friend? If not, stop saying these statements to yourself.
• Make a list of strengths. Think of what you would say about yourself if you were on a job interview.

The more we recognize our challenges with self-confidence and self-esteem, the more aware we become of improvements that can be made. This is when positive changes occur.

An Effective Teacher

What are the qualities of an effective teacher? 

Studies show nothing is as critical to a child’s education outcome than their teacher. However, in many societies the role of the teacher has been strongly critiqued. This plenary explores how we might rethink education systems so that they champion the teacher in society.

1. Knowledge of the Subject: First off, this quality is an absolute necessity to being an effective teacher. It does not matter how motivated, passionate, or creative you are if you cannot teach your students what they are there to learn. How can you expect them to learn if you don’t even know what they are supposed to be learning?
2. Motivation: To be an effective teacher one has to be motivated, motivated to learn and to help others learn. That motivation for learning and self-improvement is what separates the truly great teachers from the rest. They are always trying new ways of teaching and engaging their students and they never tire of being students themselves. Effective teachers are always learning different ways of doing things and take the time to learn from other effective teachers.
3. Emotional Intelligence and Empathy: Understanding your students is an integral part in being an effective teacher. Being able to connect with students on an emotional level and help them through the problems that come with growing up is what effective teachers do. For many kids, teachers are the ones they turn to for support when they can’t find it anywhere else. This emotional intelligence and empathy can go a long way in not only helping those students be able to learn but in changing their lives as well.
4. Stamina: As most teachers will agree, it takes a lot of energy to teach and keep students engaged. It also takes a lot of stamina, because you never know what will happen next. Every day as a teacher is an adventure, and you have to be able to handle it in stride and keep on going.
5. Passion: To me, this is the most important characteristic of an effective teacher. Passion in teachers is what inspires students to want to do their best and to dream big dreams. Passionate teachers are not those who chose to teach because they could not do anything else. Passionate teachers are those that find true happiness in their profession and in the everyday aspect of helping kids discover who they are and who they want to be.

Teachers are some of the few people who have the power to change the world because the future of the world is sitting in their classrooms. Those teachers who have knowledge, motivation, emotional intelligence and empathy, stamina, and passion are able to make an impact in the lives of their students. They inspire them to dream their wildest dreams while giving them the tools to achieve them and those are the ones who have the greatest impact.